Laboratory of Image Data Science (LIDS)

Graph-based Image Processing and Machine Learning

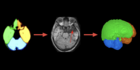
The interpretation of an image as a graph may occur at different levels where the graph nodes are pixels or superpixels. Even an image database may be interpreted as a graph whose nodes are the images or image objects. In any case, each node is represented by a set of image attributes and the arcs describe binary relations between them. In this scenario, the image operators can take advantage of a rich literature in algorithms with proof of correctness. Our aim in this project has been to reduce image processing and analysis problems into a graph problem with known algorithm. However, we are also interested in developing new graph algorithms and extending the known ones to solve real problems from several applications.

The Image Foresting Transform (IFT) has been the standard framework to reduce image partition problems, such as image segmentation, pixel clustering, and pixel classification, into an optimum- path forest problem in a graph, by choice of a suitable connectivity function (path-value function in

the graph). The IFT has also been used to the design of connected filters, distance transforms, multiscale shape representations, shape descriptors, geodesic transformations, and boundary tracking operators. Its extension from the image domain to the feature space allows the design of optimum-path forest classifiers based on supervised, semi-supervised, and unsupervised learning.

We continue to improve the Optimum-Path Forest (OPF) framework and investigate methods based on the OPF algorithm for many applications. Another goal of research here is to make the image processing operators able to learn from its errors.